Difference between revisions of "Talairach Transformation File"
m (→AC-PC to Talairach) |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
|title = Module information | |title = Module information | ||
|module = BESA Research Basic or higher | |module = BESA Research Basic or higher | ||
| − | |version = 5.2 or higher | + | |version = BESA Research 5.2 or higher |
}} | }} | ||
| Line 117: | Line 117: | ||
You want to transform an AC-PC coordinate of (-10, -78, -10). | You want to transform an AC-PC coordinate of (-10, -78, -10). | ||
| + | |||
X value: The coordinate lies in the left compartment. So: | X value: The coordinate lies in the left compartment. So: | ||
| − | + | <math> X_{tal} = x \times \frac{{LP}_{tal}}{LP} = -10 \times 1.054 = -11 </math> | |
| + | |||
| + | |||
| + | Y value: The coordinate lies in the compartment between PC and PP (we use the individual values to decide on the compartment if we transform from the individual AC-PC coordinate system). This means that we first need to subtract the length of the compartment between AC and PC in the individual coordinate system, and then stretch the remaining value in the rear Talairach compartment. At the end, we need to add the length of the compartment between AC<sub>tal</sub> and PC<sub>tal</sub> (in the Talairach coordinate system) again: | ||
| − | + | <math> y’ = y – (-PC) = -51.5 </math> | |
| − | + | ||
| − | + | <math> Y_{tal} = y’ \times \frac{{PP}_{tal} – {PC}_{tal}}{(PP – PC)} + (-{PC}_{tal}) = -51.5 \times 1.037 + (-23) = -53 – 23 = -76 </math> | |
| − | |||
Z-value: The coordinate lies in the bottom compartment. So: | Z-value: The coordinate lies in the bottom compartment. So: | ||
| − | + | <math> Z_{tal} = z \times \frac{{IP}_{tal}}{IP} = -10 \times 1.040 = -10 </math> | |
==== Generate Talairach transformation (*.tal) file from BESA MRI coregistration (*.sfh) file ==== | ==== Generate Talairach transformation (*.tal) file from BESA MRI coregistration (*.sfh) file ==== | ||
Latest revision as of 14:33, 5 May 2021
| Module information | |
| Modules | BESA Research Basic or higher |
| Version | BESA Research 5.2 or higher |
Contents
Overview
The tal file contains the transformation parameters from AC-PC coordinate system to the Talairach coordinate system. The following seven points are listed:
- Item 1 AP: Distance from x-z-plane at y==AC to anterior point (AP) along the y axis
- Item 2 PC: Distance from x-z-plane at y==AC to posterior commissure (PC) along the y axis
- Item 3 PP: Distance from x-z-plane at y==AC to posterior point (PP) along the y axis
- Item 4 SP: Distance from x-y-plane at z==AC to superior point (SP) along the z axis
- Item 5 IP: Distance from x-y-plane at z==AC to inferior point (IP) along the z axis
- Item 6 RP: Distance from y-z-plane at x==AC to right point (RP) along the x axis
- Item 7 LP: Distance from y-z-plane at x==AC to left point (LP) along the x axis
Example file content:
66.885850 26.500000 102.697017 68.035304 40.421205 65.232346 64.500000
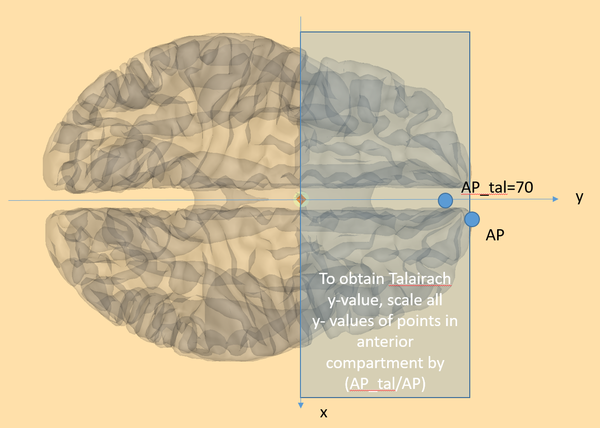
Using these points, the transformation is then performed as shown in the figure and example below.
The default values are as such (all distances in mm):
Distance AC to AP 70 Distance AC to PC 23 Distance AC to PP 102 Distance AC to SP 74 Distance AC to IP 42 Distance AC to RP 68 Distance AC to LP 68
Example of how to apply Talairach values. The principle is followed in all three directions (x, y, z). First the compartment is identified (e.g. for z axis, superior to AC, or inferior to AC). Then the coordinate is scaled with the Talairach value divided by the real value.
For the posterior compartments (y-axis), it is slightly more complicated because there are two posterior compartments: Between AC and PC, and between PC and PP. Once it is decided which compartment is the correct one, the scaling is done for this compartment only; e.g. if the compartment is between PC and PP: First subtract the relevant points from the value, i.e. [math]|y|’ = |y|-PC[/math]. Then, scale [math]y’[/math] with [math]({PP}_{tal}-{PC}_{tal})/(PP-PC)[/math]. Then add [math]{PC}_{tal}[/math]. Done!
Examples
AC-PC to Talairach
You want to transform the coordinate in AC-PC coordinate system (-38, -15, 12) to the Talairach coordinate system. The *.tal file contains the values from the above example:
66.885850 26.500000 102.697017 68.035304 40.421205 65.232346 64.500000
This means that the distances have the following relationships:
| Point | Individual value | Talairach standard | Ratio in compartment |
|---|---|---|---|
| AP | 66.9 | 70 | 1.046 |
| PC | 26.5 | 23 | 0.868 |
| PP | 102.7 | 102 | 1.037(*) |
| SP | 68.0 | 74 | 1.088 |
| IP | 40.4 | 42 | 1.040 |
| RP | 65.2 | 68 | 1.043 |
| LP | 64.5 | 68 | 1.054 |
(*): For the posterior compartment, the distance between PC and PP is used here.
X value: The coordinate lies in the left compartment. So:
[math] X_{tal} = x \times \frac{{LP}_{tal}}{LP} = -38 \times 1.054 = -40 [/math]
Y value: The coordinate lies in the compartment between AC and PC. So:
[math] Y_{tal} = y \times \frac{{PC}_{tal}}{PC} = -15 \times 0.868 = -13 [/math]
Z-value: The coordinate lies in the top compartment. So:
[math] Z_{tal} = z \times \frac{{SP}_{tal}}{SP} = 12 \times 1.088 = 13 [/math]
Transforming an AC-PC coordinate
You want to transform an AC-PC coordinate of (-10, -78, -10).
X value: The coordinate lies in the left compartment. So:
[math] X_{tal} = x \times \frac{{LP}_{tal}}{LP} = -10 \times 1.054 = -11 [/math]
Y value: The coordinate lies in the compartment between PC and PP (we use the individual values to decide on the compartment if we transform from the individual AC-PC coordinate system). This means that we first need to subtract the length of the compartment between AC and PC in the individual coordinate system, and then stretch the remaining value in the rear Talairach compartment. At the end, we need to add the length of the compartment between ACtal and PCtal (in the Talairach coordinate system) again:
[math] y’ = y – (-PC) = -51.5 [/math]
[math] Y_{tal} = y’ \times \frac{{PP}_{tal} – {PC}_{tal}}{(PP – PC)} + (-{PC}_{tal}) = -51.5 \times 1.037 + (-23) = -53 – 23 = -76 [/math]
Z-value: The coordinate lies in the bottom compartment. So:
[math] Z_{tal} = z \times \frac{{IP}_{tal}}{IP} = -10 \times 1.040 = -10 [/math]
Generate Talairach transformation (*.tal) file from BESA MRI coregistration (*.sfh) file
If you want to create a *.tal file from a BESA MRI coregistration *.sfh file to (e.g.) add a custom head-model in BESA Research 6.1, you need the Talairach transformation section in the *.sfh file:
AC: 128 128 128 PC: 167 128 128 AP: 71 124 125 PP: 240 130 143 SP: 150 47 128 IP: 210 182 122 RP: 166 128 59 LP: 170 128 202
The values for the *.tal file can be calculated as follows:
1st value: AC(x) - AP(x) = 128 - 71 = 57 2nd value: PC(x) - AC(x) = 167 - 128 = 39 3rd value: PP(x) - AC(x) = 240 - 128 = 112 4th value: AC(y) - SP(y) = 128 - 47 = 81 5th value: IP(y) - AC(y) = 182 - 128 = 54 6th value: AC(z) - RP(z) = 128 - 59 = 69 7th value: AC(z) - LP(z) = 202 - 128 = 74
The content of the *.tal file is then:
57 39 112 81 54 69 74