Cluster Alpha vs. Neighbor Distance

Module information
Modules	BESA Statistics
Version	BESA Statistics 1.0 or higher

It is often assumed that the cluster size should be manipulated by varying the neighborhood distance. While this is possible, it is not 100% correct. Cluster size should be manipulated by using the "Cluster Alpha" value, i.e. the alpha level that determines, if a sampling point will be included in the cluster or not. A higher "Cluster Alpha" value (e.g. p = 0.1) will lead to larger clusters, a smaller "Cluster Alpha" value (e.g. p = 0.001) will lead to smaller clusters, as the entry threshold for a sampling point is thus raised. The "Cluster Alpha" value is not the chosen significance level of the permutation test! It merely determines the size of the original clusters entering the permutation.

Figure 1. Grid types: regular grid (left) and irregular grid (right)

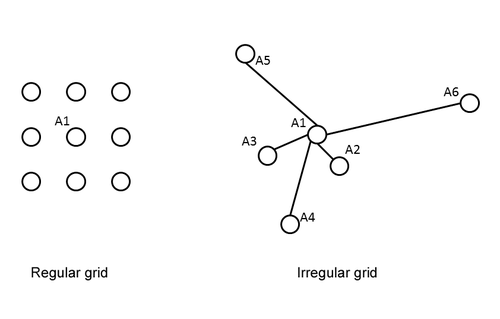
The idea of the "Neighbor Distance" is to define neighborhood (neighbor relations) of a given node (in our case a node could be an EEG/MEG channel or a voxel in the volume conductor). In the case of voxels, the grid used within the volume conductor (the head model) is a regular grid (see Figure 1 left) and the direct neighbors of a given node are uniquely defined – all nodes directly accessible from the current node (i.e. there are no nodes between the current node and its neighbors).

In the case of EEG/MEG data, the channels are not in a regular grid but in an irregular one (see Figure 1 right) and the neighbors of node A1 (see Figure 1 right) are not uniquely determined. It could be that only A2 is a neighbor of A1 or it could be that all nodes are defined as neighbors of A1. That is why it is necessary to manually define a radius (neighborhood distance) that includes all neighbors of node A1. One could choose a large radius like 100 cm. This makes no sense, however, because this way a direct connection between all nodes would be established. This could theoretically lead to a cluster of one left ear electrode and one right ear electrode – without any real connection in between.

The idea of the neighbor distance is to connect each node with its direct neighbors. Since the grid in sensor level data is not equidistant, a manually chosen distance will yield a different number of neighbors for different nodes but this is not critical.

How to determine the size of a cluster?

The first possibility is to define the cluster size as the number of points (time samples, voxels and channels) belonging to a given cluster. Then if you use a denser grid you are going to get greater clusters (i.e. clusters with more grid points). Such a measure has no statistical significance. There is another possibility for measuring the size of a cluster which could be more interesting than the previous one. That is the cluster value – it is a value used as a measure for the statistical relevance of the cluster.
In BESA Statistics this is a sum of all t-values resulted from the preliminary statistics belonging to points of the current cluster. But this value is also relative and could be useful only in the current comparison and not between different statistical comparisons. For example, a cluster value of 500 could be highly significant in the current comparison and in another project could be not significant at all. That is why we don’t report this value but we use it for the construction of the non-parametric probability distribution. The value which is useful in this context is the p-value. This value is comparable between the different experiments and comparisons and within a single comparison one could say that small p-values correspond to large cluster values, i.e. the p-value could be used as a measure for the statistical size of a cluster.
The best way to understand the statistical parameters is to play with them and see what happens. If you use Cluster Alpha = 0.05 and the whole brain is determined as a single cluster then you have to use lower alpha value (e.g. 0.01), or if your neighbor distance is 3 cm and this yields 0 neighbors in average then you have to increase it until the number of neighbors becomes e.g. 3 or more (depending on your electrode montage).